Visualization of 3D incompressible flows

see arXiv:1304.1884

Decompose a 3D divergence free velocity field into 3 components:

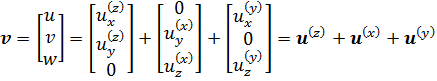
So that two dimensional divergence of each component vanishes:

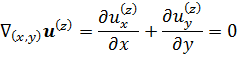
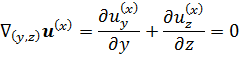
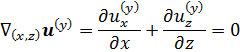
Now, for each component define vector potential, which contains only one non-zero component:

,

,

,

Therefore, non-zero components of vector potentials are extensions of two-dimensional stream function: vectors of are tangent to isosurfaces of , respectively.

Visualization of lid-driven flow in a cube

lid moves parallel to a wall, Re=1000;

lid moves parallel to the diagonal, Re=1000: in (x,y,z) coordinates; main circulation perpendicular to diagonal plane

Visualization of natural convection in a laterally heated cube

Adiabatic horizontal and spanwise boundaries: Ra=10³ Ra=10⁴ Ra=10⁵ Ra=10⁶ Ra=10⁷ Ra=10⁸

Conducting horizontal boundaries: Gr=2.9×10⁶

Isothermal surfaces at different boundary conditions

Animation of slightly supercritical oscillatory flows. Thermally conducting horizontal boundaries, Gr=3×10⁶.

Thermally conducting spanwise boundaries.

Multiple solutions for thermally insulated spanwise boundaries: Regime 1, Regime 2